Mathematical Literacy
Integrating Literacy Development
Opportunities in Your Instruction
A few years ago I attended a professional development seminar designed to help American math teachers integrate best practices and strategies required for their students to be successful with the Cambridge IGCSE program. I was a guest “reference-source,” in the seminar because of the success my students experienced in the program over the prior six years.
The IGCSE program is, in short, a college preparatory program. By passing the end of course examinations students can demonstrate college readiness. In my school they’re even given a high school diploma at the end of their 10th grade year, upon successful completion of the program of course. Some have even exited the school to attend college during what should’ve been their 11th grade year.
At the end of the seminar participants were invited to ask questions. A teacher, quite frustrated, asked, “How am I supposed to get my freshmen prepared for calculus by their senior year? There are too many things to teach and not enough time.” (What she was getting at is that the Cambridge curriculum is appears sparse compared to typical American curricula. In 9th and 10th grade there are a total of 10 topics for math.)
The presenter asked me to handle the question. I knew the answer, but could not articulate my thinking in a concise fashion. She and I were speaking different languages. I tried to explain that she didn’t have to teach everything. It is better to have a solid foundation that can be applied to all of the tangential and “one-off” topics in math, than it is to have brief experience with all of those various topics. We do not have time for both. We cannot develop deep understanding of the fundamentals of Algebra and have students exposed to all of the iterations and applications.
All she heard was a know-it-all teacher bloviate about some theoretical ideal. She needed practical advice. While I tried to provide that advice, I failed, miserably, to do so. I realized after writing this article that this information, in this article, is what I should have shared with that teacher.
Her question had a specific context, but I believe it hit the heart of one of the biggest issues faced by mathematics teachers, world-wide.
How do I get my students to acquire and retain mathematical thinking?
I’m going to offer a two-word solution: Mathematical Literacy.
If we want our students to really learn mathematics and be flexible enough to apply that knowledge in their futures, they have to be mathematically literate. Mathematical literacy, for our purposes here, is (1) the ability to decode information from mathematical text and (2) the ability to encode contextually relevant information in mathematical text.
A mathematically literate person can understand mathematics as it is written, but also realizes countless associations, contextual meanings, and tangential ideas. When a mathematically literate person sees mathematical text, they don’t wonder what should be done. They read it as information, which is decoded and analyzed. They are able to articulate appropriate, contextually relevant mathematical responses to information provided. A student that has developed this literacy is prepared for whatever type of math their futures may hold. They’re not bound by our efforts, they’re not reliant on what we have directly shown them. Instead, they’re empowered with the ability to think and communicate mathematically.
The prior two paragraphs are entirely insufficient for defining mathematical literacy. This article is about developing mathematical literacy, not defining it. If you’re interested in learning more about what is meant by mathematical literacy, consider listening to the On Teaching Math podcast on mathematical literacy. You can access the podcast with this link.
The development of mathematically literate students involves two components. First, students must make sense of problems they’ve never seen, and problems that often expose a misconception created by a person overly reliant on procedural proficiency. Then, students must apply something they know that is contextually relevant to the problem at hand. The key component here is they must identify the relevant concept and understanding. They must make the association. They cannot be following a mapped-out procedure or following instructions.
In order for this to happen, students must have a certain degree of conceptual understanding and procedural proficiency. However, marginal proficiency with both is sufficient. Through developing literacy, they will improve their conceptual understand and their procedural proficiency.
Warning: Carefully acclimate students to answering questions designed to improve literacy. If you do the thinking, instead of teasing it out from them, you can destroy the possibility of developing literacy in students. As we dive into a few examples we will discuss, in detail, how this works. But, for now, understand that if you demonstrate how to solve the problem, or answer the question, students will not develop literacy. In order to develop literacy, students need to bring in relevant conceptual understanding (may or may not be directly related to the topic being taught), and then devise a plan and monitor the appropriateness of their approach as they work through it.
If we, the teachers, make all of the connections and do all of the decision making, we’re the ones exercising our own literacy. Literacy will not be developed through imitation.
Let’s get into how we can set up experiences for our students that will promote the development of mathematical literacy. We will use solving simple polynomial equations in Algebra 1 as our initial testing ground. View these examples in their spirit, not specific application so that you can begin to craft your own questions and design their implementation.
Suppose your students have been taught how to combine like terms, and then solve simple equations, like 3x + 3 + 4x – 5 = 23. You can run them through countless pages of practice where they’d see every possible iteration of this type of problem. But, you’d not be increasing their literacy or developing a deeper conceptual understanding. That would only promote procedural proficiency, which is of course not well retained over time.
Instead, you could give students a problem like Problem A.
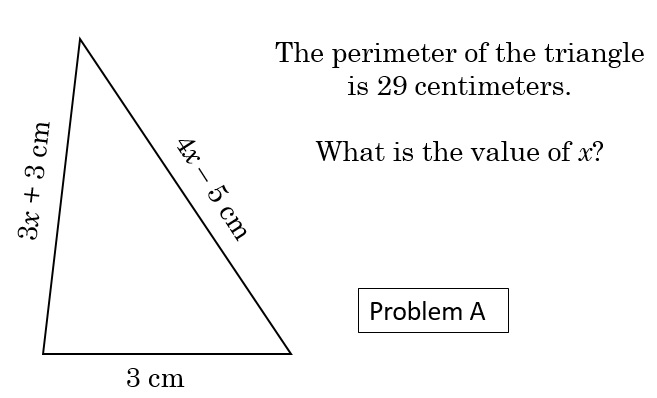
The problem on its own will not promote literacy. How you introduce the problem and your expectations of students will promote mathematical literacy. If you work a similar problem, by changing the numbers, the students will latch onto the procedure. They will not be pulling in various mathematical understandings they possess that are contextually relevant.
However, without support, at least initially, students will likely be unable to even approach this type of problem. The level of performance and thinking required of your students is likely brand new, and foreign to your students. They will wait for you to show them how it goes, and then try to recreate what they’ve witnessed. That is exactly what we do not want.
If this was the first opportunity for my students to develop mathematical literacy, I’d explain my expectation and goal to them first. The purpose of the problem is not to find an answer, but to develop the ability to understand what is written and draw in previously held understanding. Once the understanding and associations are complete, students are practicing articulating their thinking mathematically.
The purpose of this problem is to provide students with experiences that will prepare them for unknown futures. This is practice that will help make them adaptable by teaching them how to think mathematically.
A good way to start is to show students the diagram and the information, but not the question. Ask students to brain storm about what they see, what they know, what comes to mind. They’ll often be hesitant to state the obvious things, but those obvious things are sometimes the most difficult to see and are sometimes the most important things to notice!
Once students have collaborated, through whole-class discussion collect and list ideas and observations on the board next to the diagram. Many kids will have forgotten how perimeter works. This will be a great time to shore-up that issue.
Then, after all of the observations have been recorded and discussed, show students the question. Remind them that the steps to be followed are not what is important here. Creating the steps to be followed is what’s important. We want students to write mathematically, in appropriate contextual response to information provided.
Unfortunately, once this introduction has been completed, the opportunities to develop literacy with this style of problem are long gone. The road is familiar. Students will be remembering the process instead of making mathematical connections. In response to this, teachers need to have two things at the ready.
- Students coached to fully engage with the problems. They cannot sit back and wait for the path to be clear. Finding the path amidst uncertainty is the pursuit. Once a problem has been explored, the path is found and the goal is no longer attainable.
- You need a bank of problems at the ready!
Here is another, similar, but fundamentally different problem that could be used to follow Problem A.
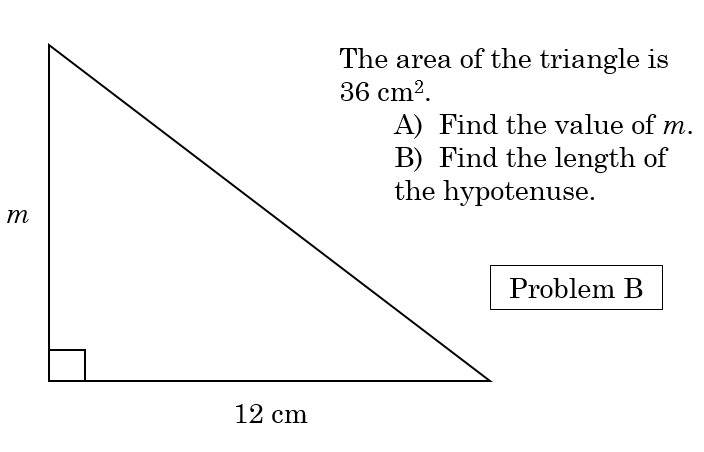
Of course helping students develop the habits of thinking that will lead to literacy takes time. You could easily teach students to “do” this problem in a handful of minutes. Then, you could try to back-fill some meaning. But then, students are learning how to “do,” the problem. They’re not getting practice learning how to thinking mathematically.
The pay-off, however, is worth the time spent! By learning how to make sense of mathematical information, and how to identify contextually important prior knowledge, then articulating their thinking mathematically, students will, over time, learn much more quickly. They will also strengthen the prior knowledge through these experiences because these experiences provide opportunity to create connections between topics. All of these benefits together result in greater retention of the new, and old, mathematical concepts.
Let’s see an example that would be appropriate for students at this level that does not involve Geometry. Again, we are considering a group of students who can distribute and combine like terms, and solve equations in one variable.
There are two boys, John and Bob. Both boys like to collect colorful rocks. Bob puts his rocks in his left pocket, which has a hole in it. John finds half of the rocks that Bob drops.
If Bob found 36 total rocks, and one third fell out of his pocket, how many of Bob’s rocks did John find?
There is nothing special about this problem, or the previous two. What is different is how you introduce the problems and how you coach students to approach the problems. Encourage brainstorming, making sense of the problems. Set the expectation that students will need to develop mathematical literacy in your class to be successful. If it is a true expectation, and you are unwavering, but encouraging, students will develop literacy over time.
Questions that are not directly related to the topic at hand can also be used. In my podcast, On Teaching Math, I start each episode off with a question like this. They’re typically easily understood and involve solutions that are within reach of most people, regardless of mathematical prowess. Also, it is often the case that the answer or discovery made by exploring the question is of little consequence. But, what is important is that students must create a hypothesis and test it, either through independent exploration or collaboration. As they test their hypothesis, through reflection they must decide to adjust their or approach, or through validation, continue on.
A typical question will be: How many times in a 24-hour period will the hands of a clock create a 90-degree angle?
Another question that is simpler is: Why is 5 the only prime number that is the sum of the previous two prime numbers?
One more example is: What number less than 100 has the greatest amount of unique prime factors?
These types of problems are a great way to give students experiences that develop mathematical literacy. The way a person must engage with those problems is the same way a mathematically literate person can engage with our last example.
One last positive outcome from these questions is that a lot of meaning will be exposed. Students will likely discover things you never thought of. That is a great outcome and a great way to include activities that promote academic discussion into your classroom.
This final example is a favorite question that can be used to develop literacy. An ancillary benefit is realized for students who failed to obtain the solution. In review, students will have a deeper understanding of exactly what the concept at hand with this topic really means.
Suppose you’ve taught your students the mechanics of functions. They can read and perform operations from examining the notation, they can perform function arithmetic, maybe composition of functions, and they can find inverse functions. I selected the words, can find, here because they indicate procedure, not concept!
Here’s the question: Given that f(x) = 2x, what is the value of x when f -1(x) = 4?
When I first saw this question on a Cambridge IGCSE examination I thought the question was entirely unfair! In fact, I was asked by a person outside of my district how kids could solve this. The students taking the test had no experience with how to find the inverse of the function!
When the test results were released I was shocked to see that the majority of my students answered the question correctly. I could not believe it. Upon questioning, students explained that the question was easy because the input and output for a function and its inverse are reversed. For example, if g(2) = 3, then g-1(3) = 2. So, if the output of the inverse of function f is four, then the input for the function f is four. Then, f (4) = 24, which is 16.
Because the students understood the concept and had practice applying concepts in new ways, they were successfully able to answer a difficult question correctly! To make it even better, they answered a question that I had never dreamt of before. This is a great example of the power of mathematical literacy.
Let’s pull it all together here. To develop mathematical literacy students must apply conceptual understanding in non-routine applications. This will likely be a shift in engagement for students and teachers. As such, we, the teachers, must orchestrate a series of experiences that will help students make this shift. We start students off with simple to understand questions that are non-algorithmic in nature, and gradually move to more complicated application of the concepts at hand. All the while, we increasingly move students to more independent thinking, where they collaborate AFTER they've have created and executed a plan. The pay-off is well worth the time and effort required! This is absolutely a case where going slow early can speed things up over time!
Your devotion and consistent application are required to help students develop mathematical literacy. You will need to incorporate these style of problems and the appropriate pedagogy into your lessons. Students will need opportunities to practice their literacy on homework, quizzes and tests. Many of the students will require continual encouragement and reiteration of the relevance of their efforts (why it is important for them, that they develop literacy).
If your students develop mathematical literacy under your tutelage, then you will have served the future needs of that student well. They will be prepared for an unknown future because they will be empowered with the ability to think, and communicate, mathematically.
If you are looking for questions that can be used to promote mathematical literacy within the application of a specific topic in math, please leave me a comment below. I have a large collection of these types of questions built over the years.
