There are many topics in math that are difficult for students to grasp because either the concept itself is elusive and maybe they don’t have the foundation required, or the procedures are complicated and riddled with traps. Algebraic Fractions or Rational Expressions, whichever name you prefer, is a great example of a topic that hits both of those.
Algebraic Fractions are intimidating from the get-go. Students see fractions with algebraic expressions and their heads practically explode! Where as exponents, are inviting and seemingly easy, at first anyway. But as students get into more complicated problems involving Algebraic Fractions, the path becomes clearer. To find a common denominator first find the LCM of the denominators, multiply each term, reduce and then combine like terms. To finish it up, reduce if possible by seeing if a GCF exists between all terms. If one exists, divide it out of all terms and done!
Once students get away from some of the basic properties and have to combine several ideas involving exponents together at the same time the students are hopelessly lost. An expression with exponents that needs to be simplified that might involve negative bases with negative exponents that are written in the denominator, then combining like-bases with the properties of exponents all while trying to traverse the muddy lines separating the order of operations (PEMDAS) when sometimes the first three (P, E, and M) are completely interchangable because it’s all multiplication, where other times you must take care of the group first and the multiplication last. It’s over-whelming and all comes back to my favorite harping point, the ability to read mathematics by understanding the meaning behind how it is written.
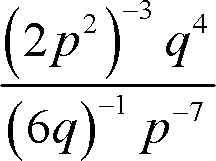
While I work very hard to build a strong conceptual foundation for my students, sometimes I start doing the framework of the house before the foundation has has time to set. This is often the case with Algebraic Fractions. But, if their procedural fluency is sufficient, they can often repair their weaknesses in the foundation, or never need to shore it up at all and suffer little, if any, from it.
There are other topics that can be taught with concept only, for example, graphing a linear equation by finding the intercepts. If students know what intercepts are, know how to find their coordinates, and know that linear equations are equations whose solutions form a line, they can put all of that together on their own.
Exponents are different. The basic properties of exponents can be taught without covering the “rules” at all. By simply knowing that exponents are repeated multiplication, and writing things out, students can get quite a long way. I’d suggest they can get through division like the problem below without using the “Negative Exponent Rule.”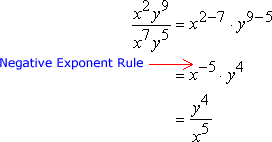
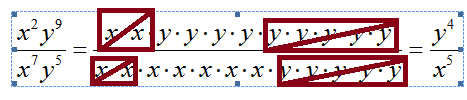
Now this is not a practical way to go about simplifying an expression. The rules, or properties, prevent students from having to reinvest the wheel, as it were. However, if the rules are introduced too soon, before the foundation has set and hardened, then with exponents, there will be serious troubles ahead. And yet, visualizing this method displayed above, without using the properties to obtain the answer by some procedure, allows one to visualize that there are two more x’s in the denominator and four more y’s in the numerator.
But without a measurable level of fluency with applying the rules of mathematics, simplifying expressions involving exponents quickly becomes insurmountable. Consider a problem with multiple brackets, rational exponents, negative bases and negative exponents, like the one below. This would be overwhelming to approach with only a conceptual understanding, but no applicable short cuts in the proverbial tool box.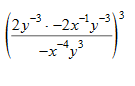
With exponents it is imperative that a balance between the ability to approach any problem from a conceptual framework or to approach the same problem from a procedural framework with equal accuracy, must be achieved. Students with strong conceptual understanding but little practical procedural ability will struggle with a similar level of difficulty compared to students with little conceptual understanding but that are well versed in the “rules” of exponents.
Students and teachers are very accustomed to seeking and rewarding answer-getting techniques. This is what makes exponents a wonderful topic to spend a lot of time on. You can show students how focus on procedure alone is insufficient, and how multiple methods of finding solutions is a powerful tool because combined with a little experience clear paths to solutions unfold when there is no proper first step.
An example of a problem without a proper first step is below:
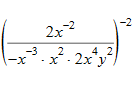
There are many, equally efficient, and mathematically correct ways to begin simplifying such an expression. Students that rely on procedures will struggle mightly with these types of problems because the first step depends on what you recognize first (conceptual understanding). How to respond to what is first recognized depends on the procedural fluency of the student.
It is a great exercise to take a problem like this and have one student perform some operation of their choosing, then another to perform a second operation and so on, until the problem is simplified completely.
By exposing students to problems where the initial step is highly variable and the method of arriving at correct answers vary upon what is noticed by students, they can develop a sense that math works this way.
Students should not consider math to work as follows: Well, this problem looks like the last problem we did and I used the quadratic formula last time, so let’s do that.
It is my intent that when teaching something like exponents (and radical expressions can be similar) I am trying to plant the seed of this idea that math can be approached from many points of view, and sometimes, the right answers are not so cut and dry.
I am currently working on a series covering exponents, square roots and rational expressions where both the needs of the student are addressed through tutorial/remediation videos, and instructional coaching, lessons and practice problems for teachers. The videos will be posted here on this website, but also on my YouTube channel. The lesson will serve to meet two callings. First, students have conceptual understanding of the topics and procedural fluency, but both done in a way that promotes mathematical literacy.
If you are interested in such a treatment of exponents, done in a way to encourage to view mathematics in a different light entirely, you can subscribe to my newsletter, or visit my YouTube channel and subscribe there. Either way, I’m finishing up the series on exponents soon and will post them when done.
Thank you for reading. And please, if you found this to be informative or useful, spread the word.
Philip
WE NEED THE HARDer QUESTIONS POR FAVOR .